
Dynamic Programming 기초1 - Fibonacci
개요
피보나치 수열의 3가지 구현방법을 알아본다.
- Simple Recursion
- Recursion with Memoization
- Bottom-Up Approach
피보나치 수열
0, 1, 1, 2, 3, 5, 8, 13, 21...
nth value = (n-1)th + (n-2)th 의 방식으로 전개되는 수열이다. 재귀함수로 구현할 수 있다.
private static long fibSimple(int n) {
return (n < 2) ? n : fib(n-1) + fib(n-2);
}
기존 Recursion 의 문제점
Recursive 하게 짠 fib() 함수는 아래와 같은 방식으로 호출이 일어난다.
n=5 일 때 벌써 함수 호출을 15번이나 해야 한다. n이 작을때는 문제 없지만 n이 커졌을 때 2가지 문제점을 발견할 수 있다.
- 재귀호출이 지나치게 많아져서 memory 가 부족해 질 수 있다.
- 함수가 호출되고 return 하기 전까지는 memory 의 stack 영역에 돌아갈 곳을 기록해 둔다. n 이 커지면 커질수록 stack 에 함수 호출에 대한 기록이 더 많이 쌓이는데 return 하기 까지 또다른 재귀적 호출이 있기 때문에 문제가 생길 수 있다.
- 느리다.
- O(2n) 의 시간 복잡도를 가진다.
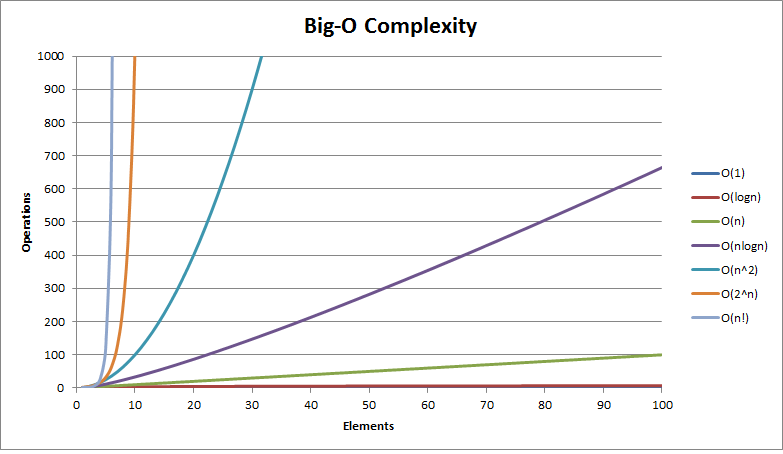
O(2n) 의 시간 복잡도를 가지는 알고리즘은 factorial 다음으로 최악의 성능을 가진다. Input 이 크다면 반드시 피해야 하는 방법이다.
해결방법1 - Memoization
Memoization 은 Dynamic Programming 의 한 방법으로 한번 계산한 값을 반복적으로 계산하지 않도록 기록해 두는 것이다.
기존 recursion 방식은 재귀호출 자체가 문제라기 보다는 불필요한 호출을 여러번 하게 된 다는 것이다. fib(5) 를 구하기 위해 fib(3) 은 2회, fib(2) 는 3회, fib(1) 은 5회… 호출하게 된다. Memoization 의 아이디어는 처음 fib(n) 을 계산할 때 어딘가에 기록해 두고 또 사용하게 될 경우에는 기록해 둔 결과값만 가지고 오는 것이다. Memoization 을 사용했을 때의 recursion tree 는 아래 그림과 같다.
private static long fibMemoization(int n, long[] memo) {
if (memo[n] != 0) return memo[n]; // 기록해 둔 것이 있으면 사용
memo[n] = (n == 1 || n == 2) ? 1 : fibMemoization(n-1, memo) + fibMemoization(n-2, memo); // 기록해 둔 것이 없으면 계산하고 기록
return memo[n];
}
Memoization 을 사용하는 호출의 경우 상수시간이 걸리고, 첫번째 fib(n) 을 계산 할 때만 재귀적 호출이 두번 f(n-1) + f(n-2) 이루어지기 때문에 O(2n + c) = O(n) 의 time complexity 를 가진다. 기존 O(2n) 에서 O(n) 으로의 개선은 큰 변화다.
해결방법2 - Bottom-Up
Recursion 을 사용하지 않는 방법. 상대적으로 memory 를 적게 사용한다. Recursion 이 top-down 이라면, bottom-up 은 말 그대로 작은 것 부터 순차적으로 풀어나간다.
풀이방법은 간단하다. 1st, 2nd, 3rd element 는 직접 지정해주고, 4th element 부터는 array[n-1] + array[n-2] 를 계산한다.
private static long fibBottomUp(int n) {
long[] bottomUp = new long[n+1];
bottomUp[1] = 1;
bottomUp[2] = 1;
for (int i=3; i<=n; i++) bottomUp[i] = bottomUp[i-1] + bottomUp[i-2];
return bottomUp[n];
}
이 방법 역시 from 3 to n 까지 한 번의 loop 만 수행하면 되므로 O(n) 의 시간복잡도를 가진다.
Comparison
위 세가지 방법을 thread 에서 동시에 실행 시키고 execution time 을 milliseconds 단위로 측정해 보았다.
public class Fibonacci {
public static void main(String[] args) throws Exception {
int N = 50;
long[] memo = new long[N+1];
Thread fibSimpleThread = new Thread(() -> {
long startTime = System.currentTimeMillis();
System.out.format("fibSimple: %d %n", fibSimple(N));
System.out.format("fibSimple elapsed time: %d ms%n%n", (System.currentTimeMillis() - startTime));
});
Thread fibMemoizationThread = new Thread(() -> {
long startTime = System.currentTimeMillis();
System.out.format("fibMemoization: %d %n", fibMemoization(N, memo));
System.out.format("fibMemoization elapsed time: %d ms%n%n", (System.currentTimeMillis() - startTime));
});
Thread fibBottomUpThread = new Thread(() -> {
long startTime = System.currentTimeMillis();
System.out.format("fibBottomUp: %d%n", fibBottomUp(N));
System.out.format("fibBottomUp elapsed time: %d ms%n%n", (System.currentTimeMillis() - startTime));
});
fibSimpleThread.start();
fibMemoizationThread.start();
fibBottomUpThread.start();
}
private static long fibSimple(int n) {
return (n < 2) ? n : fibSimple(n-1) + fibSimple(n-2);
}
private static long fibMemoization(int n, long[] memo) {
if (memo[n] != 0) return memo[n];
memo[n] = (n == 1 || n == 2) ? 1 : fibMemoization(n-1, memo) + fibMemoization(n-2, memo);
return memo[n];
}
private static long fibBottomUp(int n) {
long[] bottomUp = new long[n+1];
bottomUp[1] = 1;
bottomUp[2] = 1;
for (int i=3; i<=n; i++)
bottomUp[i] = bottomUp[i-1] + bottomUp[i-2];
return bottomUp[n];
}
}
N 이 50만 되어도 실행 시간은 아래와같이 크게 차이 난다. 단순하게 재귀로 접근한 방법보다 memoization, bottom-up approach 를 사용한 dynamic programming 방식이 (N=50 일 때) 약 2880배 빠르다.
fibMemoization: 12586269025
fibMemoization elapsed time: 25 ms
fibBottomUp: 12586269025
fibBottomUp elapsed time: 25 ms
fibSimple: 12586269025
fibSimple elapsed time: 72173 ms
Process finished with exit code 0
계산 결과가 맞는지는 여기 로 가면 n=300 까지의 피보나치 수를 확인할 수 있다.