Graph
개요
- Graph 관련 용어
- Graph 를 표현하는 세 가지 방법
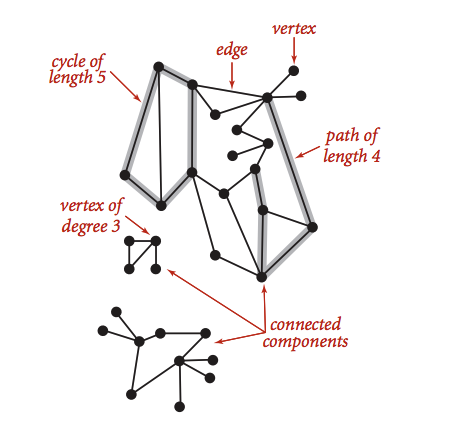
용어
| Graph | Edge 와 Vertex 로 연결된 Set |
| Degree(차수) | Vertex 에 연결된 Edge 의 갯수 |
| Path | Edge 로 연결된 Vertex 들의 Sequence |
| Cycle | 첫 Vertex 와 마지막 Vertex 가 같은 Path |
| Connected | 임의의 Vertex 들 간에 Path 가 존재하면 Connected |
그래프 관련 질문
- V1 과 V2 사이에 Path 가 존재하는가?
- V1 에서 V2 로 가는 최단 경로는?
- 사이클이 있는가?
- 각 Edge 를 정확히 한번만 방문하는 사이클이 존재하는가? - Euler tour
- 각 Vertex 를 정확히 한번만 지나는 사이클이 존재하는가? - Hamilton tour
- 모든 Vertex 를 연결시킬 수 있는 방법이 있는가? - Connectivity
- 모든 Vertex 를 연결하는 최적의 방법은 무엇인가? - MST
- 임의의 Vertex 제거할 경우에 Connected 그래프를 Disconnected 그래프가 되게 만드는 Vertex 가 있는가? - Biconnectivity
- 교차하는 Edge 가 없도록 그래프를 표현할 수 있는가? -Planarity
- 두 개의 인접한 리스트는 같은 그래프를 표현 하는가? - Graph isomorphism
그래프를 표현하는 3가지 방법
Set of Edges
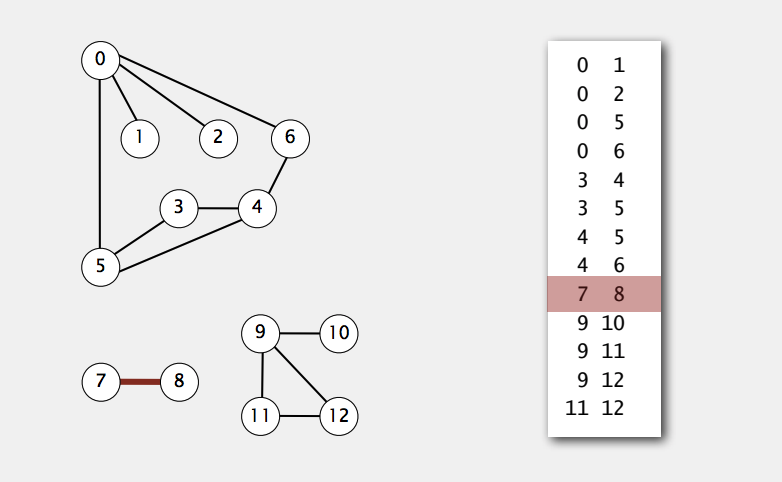
각 edge 들이 어떤 vertex 에 연결되어 있는지에 대한 정보들만 가지고 표현하는 방법. 거의 쓰이지 않는 방식.
Adjacency Matrix
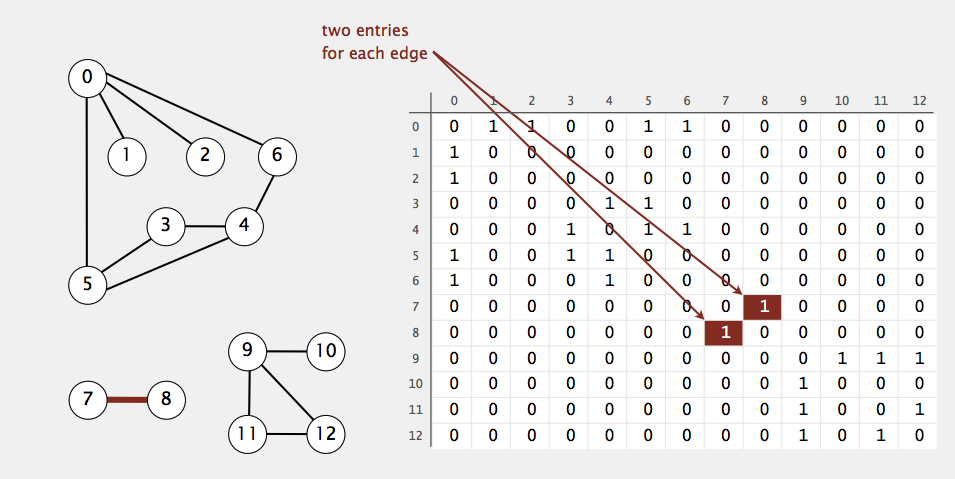
인접행렬. (7)-(8) 의 경우에 adj[7][8] = adj[8][7] = true 의 형태로 표현 됨. Degree 가 높은 dense 한 vertex 들을 가지는 그래프에서 유용하지만 sparse 한 그래프의 경우 메모리의 낭비가 심함.
Adjacency List
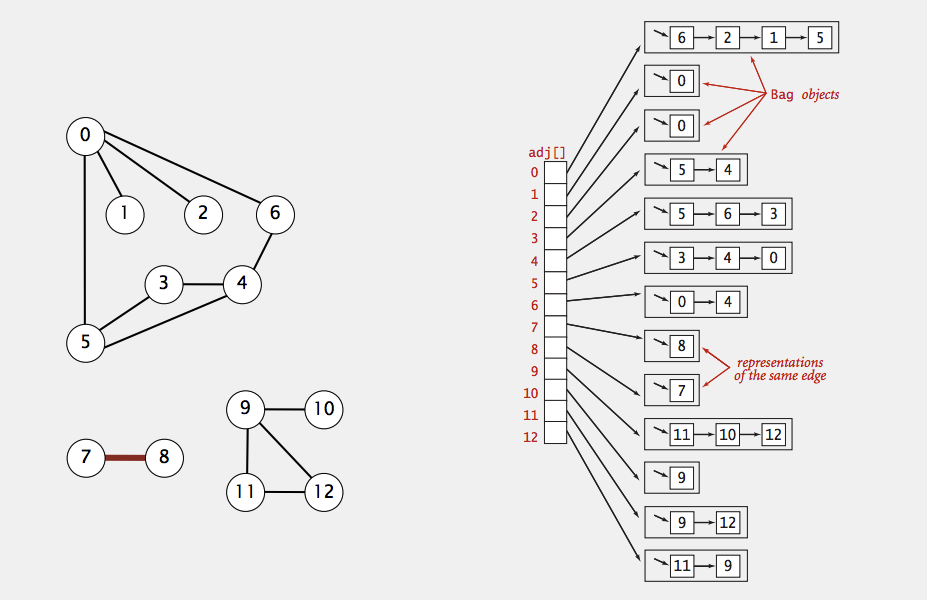
인접 리스트로 표현하는 방법. 대부분의 경우 실전에서 그래프를 표현 할 때는 이 방식으로 사용. 실제 그래프의 경우 dense (degree 가 높은) 한 경우 보다 sparse (degree 가 낮은, vertex 는 많아도 각 vertex 에 연결된 edge 수는 적은) 한 경우가 일반적.
구현
Coursera 강의에서는 LinkedList 가 아닌 Bag 이라는 데이터 구조를 사용하는데, 그냥 LinkedList 를 사용해서 구현했다.