Binary Tree 종류 - Heap 구현 사전지식

by Yaboong on February 10, 2018

개요

Heap 구현을 위한 Binary Tree 의 기초적인 개념에 대해 알아본다.

Binary Tree

Binary Tree 에는 여러 종류가 있지만 Heap 구현을 위해서 알아야 tree 는 Complete Binary Tree 이다. 기본적인 tree 의 형태로는

• Full Binary Tree
• Perfect Binary Tree
• Complete Binary Tree
• Degenerate (or Pathological) Tree

Full Binary Tree

Full Binary Tree

• 모든 노드가 0개 혹은 2개의 children 을 가지고 있을 때 “Binary Tree 는 full” 이라고 한다.
• 같은 의미 다른 말로, “Full Binary Tree 는 leaf 노드들을 제외한 모든 노드들이 2개의 children 을 가지는 Binary Tree” 라고도 할 수 있다.
• L = I + 1 - Full Binary Tree 에서 모든 leaf 노드의 개수는 internal node 의 개수 + 1 이다.
• L = leaf nodes (하늘색) 개수, I = internal nodes (보라색) 개수. 혹시 증명이 궁금하다면 여기 참고

Perfect Binary Tree

Perfect Bianry Tree

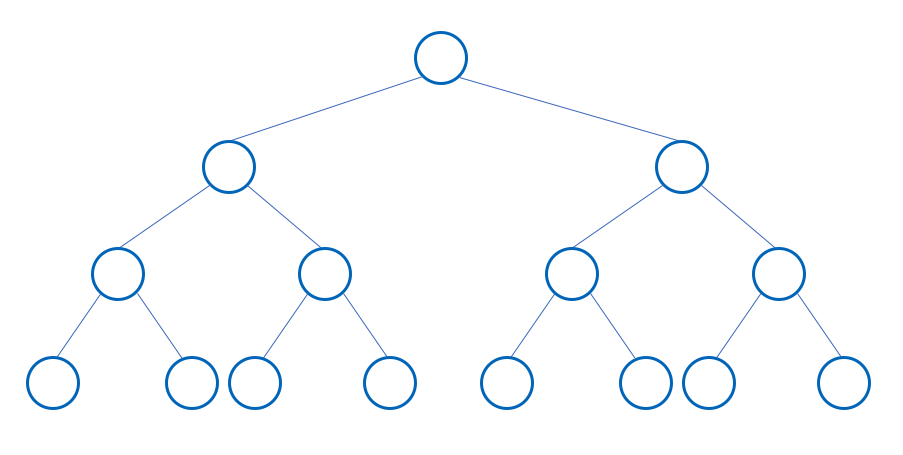
• 모든 internal node 가 두개의 children 을 가지고 있고, 모든 leaf 노드가 같은 level 에 있으면 Perfect Binary Tree 라고 한다.
• Height 가 h 인 Perfect Binary Tree 는 2^h - 1 개의 노드를 가진다.
• 위 그림의 경우 height 는 4 이고, 노드의 개수는 2⁴ - 1 = 15 개의 노드를 가지고 있다.

Degenerate (or Pathological) Tree

Pathological Tree (사향트리)

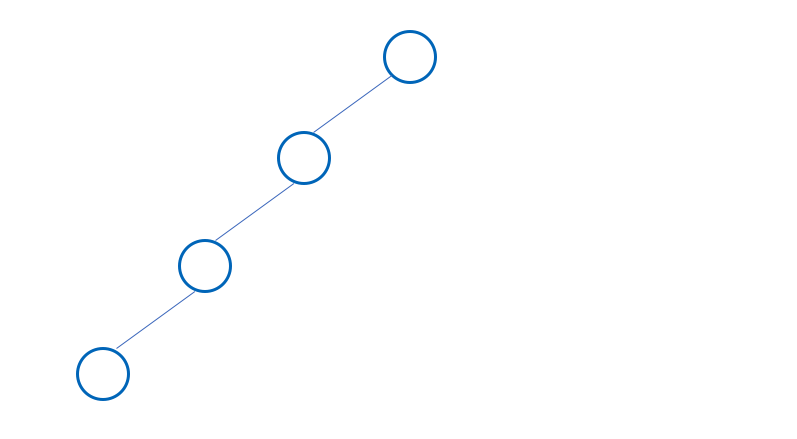
• 모든 internal node 가 하나의 child 만을 가질 때 Degenerate (or Pathological) Tree 라고 한다.
• Linked List 성능과 동일하다.

Complete Binary Tree

Complete Binary Tree

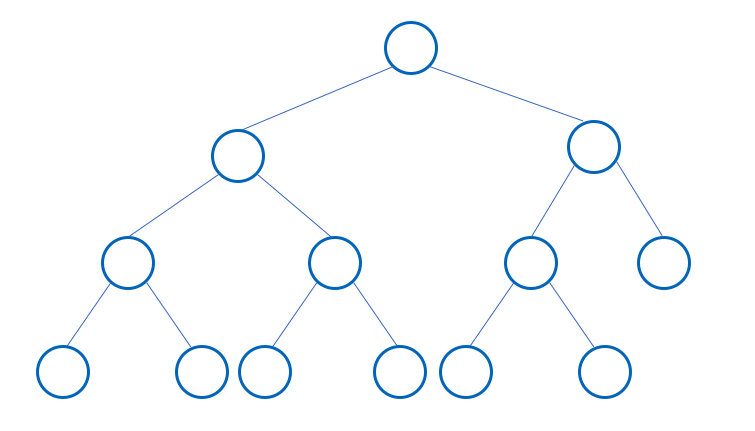
• 마지막 level 을 제외한 나머지 level 에 node 들이 가득 차있고, 마지막 level 에서 node 는 가장 왼쪽 부터 채워지는 형태가 Complete Binary Tree 이다.
• Complete Binary Tree 구조를 그대로 사용하여 Binary Heap 이라는 데이터 구조를 만들 수 있는데, 이놈이 Heap 이다.
• Complete Binary Tree (15개의 데이터가 저장된다면 index 0 ~ index 14 까지 채워진다) 구현에는 Array 를 사용하는 것이 일반적이다.

정리

• Heap 은 Complete Binary Tree 형태를 가진다.
• Complete Binary Tree 구현에는 Array 를 사용하는 것이 일반적이다.
• Heap 은 Array 를 사용해서 구현하는 것이 편하다.

참고한 자료

• https://www.geeksforgeeks.org/binary-tree-data-structure/