
Depth-First Search & Path
개요
- Graph 의 탐색 방법인 Depth-First Search (깊이우선탐색) 알고리즘에 대해 알아본다
- Depth-First Search 메소드 구현
- DFS 응용 - 임의의 노드 v 에서 w 로 가는 path 가 있는지 알아보는 메소드 구현
- 코드 보기
Depth-First Search (깊이우선탐색)
그래프 또는 트리의 탐색에는 크게 깊이우선탐색, 너비우선탐색 두가지 방법이 있다. 탐색이라하면 각 vertex 들을 한번씩만 거치고 모든 vertex 를 순회하는 것을 말한다. 이번 포스팅에서 볼 내용은 깊이우선탐색 (DFS) 이다.
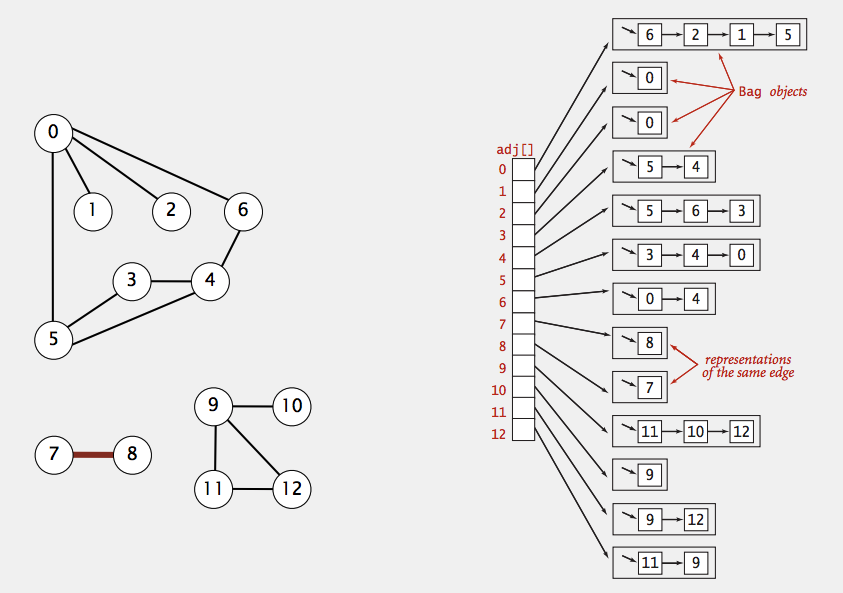
그래프는 인접리스트를 이용해 위와같이 표현할 수 있다.
DFS 는 인접리스트의 vertex 중 이미 방문하지 않는 vertex 를 만나면 바로 그 vertex 의 인접리스트를 방문하러 간다. (재귀적 호출)
위 그래프를 예로, 0 부터 시작해서 dfs 가 호출되는 과정을 앞 부분 조금만 살펴보면 처음에 0 부터 시작했으므로 adj[0] 의 연결리스트들인 6 -> 2 -> 1 -> 5 를 순서대로 방문한다. 시작인 0 번 노드 다음엔는 6번 노드를 방문하게 된다. 6번을 방문했음을 표시하고 2번 노드로 가는 것이 아니라 (2번 노드로 가는 것은 BFS), adj[6] 의 연결리스트 를 살핀다. adj[6] 의 연결리스트를 보니 0 -> 4 가 있다. 0 은 이미 방문 했으므로 이번에는 4번 노드로 가도 된다 (0을 이미 방문하지 않았더라면 adj[0] 의 연결리스트를 봐야 했을 것임). 4번 노드를 방문했음을 표시하고 adj[4] 의 연결리스트를 보면 5 -> 6 -> 3 을 방문하는데 이때 5 는방문하지 않았으므로 adj[5] 의 연결리스트를 살핀다.
위 과정을 보면 재귀적으로 호출이 이루어지는 것 같은 감(?) 을 잡을 수 있다.
아래 슬라이드를 참고하며 볼 때 adj[0] ~ adj[6] 까지 인접리스트를 노트에 그려두고 방문한 노드는 엑스표시를 쳐 가면서 함께 보면 이해하기 편하다. 방문한 노드를 표시하기 위해 marked 이름의 배열을 사용한다. edgeTo[] 배열은 어떤 임의의 노드를 처음 방문할 때 어느 노드를 통해서 왔는지에 대한 기록을 남겨두는 것이다. 첫 방문시 바로 직전 노드를 기록한다고 생각하면 된다. 좀 더 아래에서 v 에서 w 로 가는 path 가 있는지 알아보는 메소드를 작성할건데 이 때 edgeTo 배열을 활용한다.
구현 - Java
DFS 의 구현은 생각보다 간단하다.
public void dfs(int v) {
marked[v] = true;
System.out.println(v);
for (int w : adj[v])
if (!marked[w]) {
dfs(w);
edgeTo[w] = v;
}
}
dfs 를 호출할 때 방문했음을 marked 배열에 표시해주고 해당 노드를 출력한다. 그리고 해당 노드의 연결리스트를 보고 다음 노드를 방문하지 않았으면 다음 노드에서 또 dfs 를 재귀적으로 호출해준다. 이때 edgeTo 에 대한 표시는 다음 dfs 를 호출하기 전에 하든 dfs 호출 이후에 하든 상관없다. 하지만 (이전 노드에 대한 정보가 없기 때문에) marked = true 를 표시해주는 곳에서 같이 해 줄 수는 없다.
marked, edgeTo 배열은 Graph 클래스의 생성자에서 노드의 갯수에 맞게 초기화 해 주어야 한다.
응용 - Depth First Paths
DFS 를 응용해서 임의의 노드 source -> destination 로 가는 길이 있는지 찾는 pathFromTo(source, destination) 메소드를 만들어 보자. (DFS 를 응용해서 path 가 있는지 없는지 알아보는 것이지 최단거리를 구하는 방법은 아니다)
pathFromTo(source, destination) 에서 source = 0, destination = 3 인 경우
- 주어진 그래프에 dfs 를 한번 돌린다
- source 인 0 을 시작으로 dfs 를 한번 돌리기 때문에 0 에 연결되어 있는 노드들만 방문하게 된다
- 즉, source 에 연결되어 있지 않은 노드들은 marked[] 배열의 값이 모두 false 이다
- marked[destination] 의 값이 false 라면 source 노드에서 destination 노드로 가는 path 는 존재하지 않는 것이다
- 각 노드 처음 방문시, 방문직전에 어떤 노드를 통해서 왔는지 edgeTo[] 에 기록한다
- 1 방문시 0 을 거쳐서 왔다면 edgeTo[1] = 0 이 된다
- 0 에서 3 으로 가는 path 가 있는지 알기위해서 목적지인 3 부터 edgeTo 배열을 아래와 같은 방법으로 뒤진다 (위 슬라이드 자료의 dfs 결과인 29번 슬라이드 참고)
- stack 에 destination 노드 먼저 push -> stack.push(3)
- 3 은 어디를 거쳐 왔는지? -> edgeTo[3] = 5 -> stack.push(5)
- 5 는 어디를 거쳐 왔는지? -> edgeTo[5] = 4 -> stack.push(4)
- 4 는 어디를 거쳐 왔는지? -> edgeTo[4] = 6 -> stack.push(6)
- 6 은 어디를 거쳐 왔는지? -> edgeTo[6] = 0 -> stack.push(0)
- destination 노드부터 역순으로 source 인 0 에 도달했으므로 종료한다
- 위 과정에서 각 edgeTo 배열의 값들을 stack 에 push 하고 stack 의 결과를 출력하면 path 를 알 수 있다.
- Stack [3, 5, 4, 6, 0]
- 0 -> 6 -> 4 -> 5 -> 3
Depth First Paths 구현 - Java
private boolean hasPathTo(int v) { return marked[v]; }
public Iterable<Integer> pathFromTo(int src, int dest) {
dfs(src);
if (!hasPathTo(dest)) return null;
Stack<Integer> path = new Stack<>();
for (int x = dest; x != src; x = edgeTo[x]) // edgeTo[x] 로 x 를 업데이트
path.push(x);
path.push(src);
return path;
}
실행 예제
public static void main(String[] args) {
Graph g = new Graph(13);
g.addEdges(0, 5);
g.addEdges(4, 3);
g.addEdges(0, 1);
g.addEdges(9, 12);
g.addEdges(6, 4);
g.addEdges(5, 4);
g.addEdges(0, 2);
g.addEdges(11, 12);
g.addEdges(9, 10);
g.addEdges(0, 6);
g.addEdges(7, 8);
g.addEdges(9, 11);
g.addEdges(5, 3);
int source = 0, destination = 3;
Stack<Integer> stack = (Stack<Integer>) g.pathFromTo(source, destination);
if (stack == null) {
System.out.println("No path from " + source + " to " + destination);
} else {
while(!stack.isEmpty()) {
int item = stack.pop();
System.out.print(stack.isEmpty() ? item : item + "->");
}
System.out.println();
}
}
각 vertex 의 연결리스트가 어떻게 구성이 되었는지에 따라 예제에서 설명한 순서와 출력이 달라질 수 있다. 자바에서 LinkedList 에는 add(), addLast(), addFirst() 세 가지 메소드들이 있는데 add() 는 addLast() 와 같은 방식으로 동작한다. 위 main() 함수에서 그래프를 생성할 때 edge 를 추가하는 순서로, 처음 그림의 그래프와 똑같은 그래프를 구성하려면 addEdges() 내부에서 연결리스트를 구성할 때 add() 메소드가 아닌 addFirst()를 를 사용해줘야 한다.