
Merge Sort - 합병정렬
개요
- Merge Sort 의 divide, merge 부분 동작 파악
- 구현 - Java
- 시간복잡도 분석 - 점화식 풀이
- 코드 보기
Merge Sort
- 배열의 길이가 0 또는 1이면 이미 정렬된 것으로 본다. 그렇지 않은 경우에는
- 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
Divide
Divide 에 대한 부분은 코드에서 mergeSort() 라는 메소드가 실행한다. 재귀적으로 배열을 반씩 자르고, 길이가 0 또는 1 이 되었을 때 merge 하는 과정은 아래와 같다.
Merge
merge() 메소드가 동작하는 과정은 아래와 같다. 몇 번의 divide(), merge() 작업이 반복적으로 실행 됐고, 최종적으로 처음에 divide 했던 두개의 sub array 를 merge 하는 과정이다. 두개의 sub array 들은 각각 정렬이 되어 있는 상태다.
바로 위 슬라이드에서 마지막 merge 가 실행되는 과정을 하나씩 살펴 본 슬라이드이다.
구현
분석
Merge sort 는 O(nlogn) 의 시간복잡도를 가진다. 어떻게 그렇게 되는지 보자.
T(n) = 2T(n/2) + n
위 점화식은 merge sort 를 표현한 점화식이다. T(n/2) 는 divide 하는 과정이고 n 은 merge 에 대한 부분이다. T(n) 을 T(n/2) + n 으로 표현 가능하다면 T(n/2) 는 아래와 같이 표현 가능하다.
T(n/2) = 2T(n/4) + n/2
각각의 T(x) 를 재귀적으로 표현해보면
T(n/4) = 2T(n/8) + n/4
와 같이 표현 가능하다.
각각의 점화식을 트리구조로 표현해보면 아래와 같다.
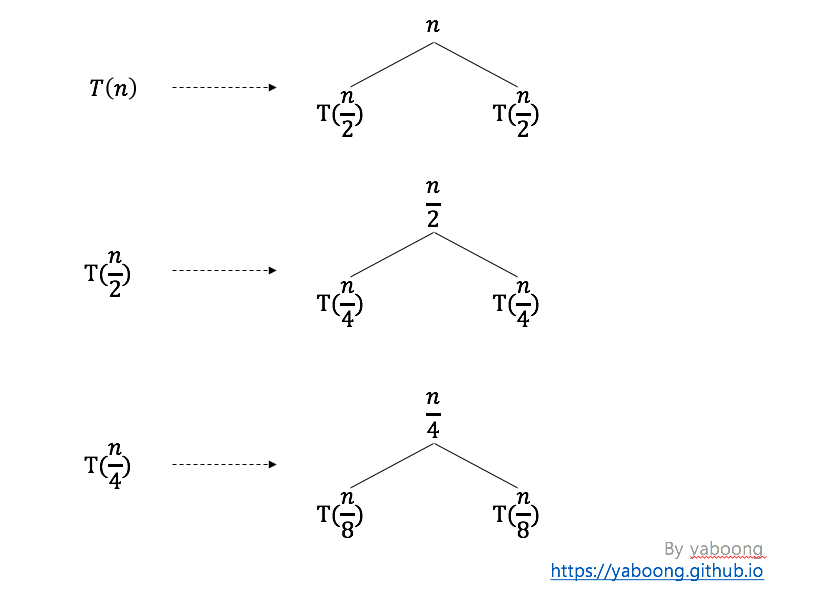
위 그림에서 T(n) 을 표현한 트리에서 T(n/2)을 T(n/2) 을 표현한 트리로 대치시키고, T(n/2) 을 표현한 트리에서 T(n/4) 을 표현한 트리로 계속해서 대치시켜 나가면 아래와 같은 트리를 그릴 수 있다.
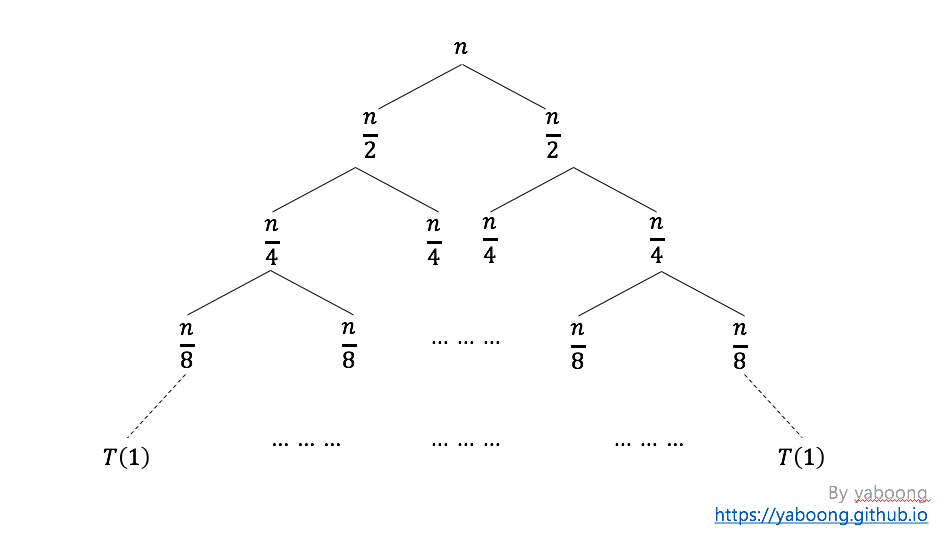
트리의 각 레벨에서 노드의 개수와, 각 레벨의 합을 구하면 아래와 같다.
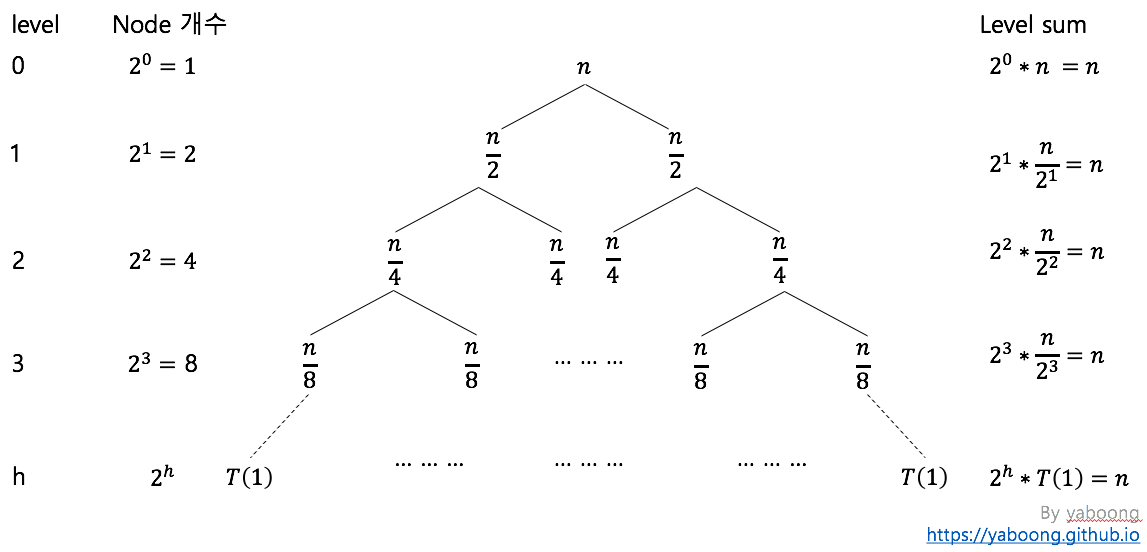
Level 0 에는 n이 1개 있고, level 1 에는 n/2 이 2개, level 2 에는 n/4 이 4개, … , level h 에는 T(1) 이 2h 개 있다. T(1) = 1 로 표현 가능하므로 h = log2n 이라는 결과를 얻을 수 있다.
2h * T(1) = n
2h = n
h = log2n
즉, 각 레벨의 합인 n 이 트리의 높이인 logn 개 만큼 있으므로, 전체 시간 복잡도는 O(nlogn) 이라는 결론을 얻을 수 있다.
비교
Coursera 강의에 재미있는 자료가 있었다. Merge sort 와 insertion sort 를 일반 컴퓨터, 슈퍼 컴퓨터로 실행한 결과에 대한 비교이다. 삽입정렬은 N 이 10억개면 317년이 걸린다.
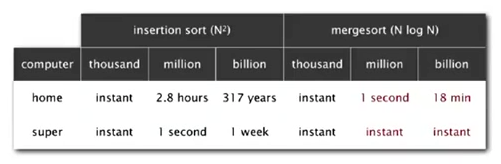
Good algorithms are better than supercomputers. – Robert Sedgewick 교수님 가라사대